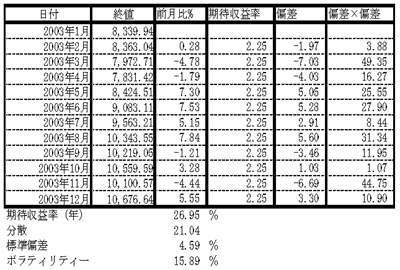
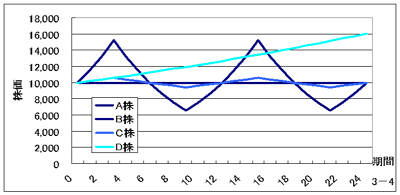
ストックオプション会計基準では、ストックオプションの公正価値を付与日時点において算定し、その後は条件変更等がなければ見直さないこととしています。しかし、そのような会計処理がなされると、場合によっては希薄化の度合いが適切に把握されないおそれが生じます。

　市場で取引されるオプション取引は、取引後も原則的には時価評価されます。もしそうしなければ、市場の動きに影響を受けるオプション価格を、満期日までの期間において正確に把握することができないからです。
　これは会社が従業員等に対して発行するストックオプションについても同様で、もしオプションの時価評価を継続的に行わなければ、権利行使時にいきなり希薄化が判明することになってしまいます。このため、付与日における費用化額は暫定的なものとし、権利行使時の公正価値を最終的な費用計上額にすべきとも考えられます。
　実際、この問題はストックオプション会計基準策定にあたっても論点とされていました。具体的には、ストックオプション会計基準50項において「ストックオプションの公正な評価単価は常に変動しているため、その算定の基準日が問題となる。」として取り上げられています。
　ところが、このような論点に対するストックオプション会計基準での取り扱いは、付与日における公正な評価単価を算定することとされました。これは、付与日以後のストックオプションの公正な評価単価の変動は、サービスの価値とは直接的な関係を有しないもの考えられているためです。つまり、企業と従業員等がともに経済合理性を有しているのであれば、ストックオプションと労働サービスの提供は等価交換されると考えられるところ、両者の交換時点は付与日であると解釈できるためです。
　したがって、現行会計基準のもとでは、ストックオプションの費用化額は付与日における公正な評価額となります。

投稿者: ストックオプション評価委員会 日時: 15:11 | パーマリンク

ボラティリティについての概念は様々な解説書の中で見ることは多いのですが、その具体的な算出方法については、きちんと解説しているものは多くないようです。
そこで、誰にでもできるボラティリティの簡易的な算出方法を解説します。

ボラティリティは観察期間の資産価格の変化率の標準偏差を算出し、最後に年率に修正します。下記例では月次の標準偏差が出します。ボラティリティは時間の平方根に比例しますので、年率にするには月次の標準偏差に√12を掛けます。

【日経平均の実際のデータ】

投稿者: noguchi 日時: 13:57 | パーマリンク

ボラティリティはオプション評価のうえで重要は基礎数値であることは誰もが認めているところです。しかし、専門家ではない限り、ボラティリティを「株価の変化の度合い」と解釈している人が多いようですが、厳密に言えば、この考え方は間違っています。

Ｑ：値動きのグラフにおいて、ボラティリティの高い順に並べよ

Ａ：A−C−B,Dの順番にボラティリティは高い。

ボラティリティは資産の変化率を表すのではなく、期待収益率からどれだけバラツキがあったかを示すものです、従ってDのように観察期間中にどれだけ資産価格が上昇しても、その上昇の仕方が一定であれば、ボラティリティはゼロとなり、全く動かなかった相場Bと同じになります。ある観察期間のスタート時の株価とエンド時の株価を、直線で結んだ経路が最短距離になりますが、その直線上を動いたとき、ボラティリティはゼロになるということです。　その最短距離に対して、どれだけ寄り道したかで、ボラティリティの大きさが決まってくるのです。これは物理学における力の考え方とよく似ています。物理学では、力がかかっていないという意味で、等速で一定方向に動いていることと静止していることは同じとみなします。ボラティリティも同様の考え方をしますので、まったく動かなかったB株と毎期間一定の上昇を続けたD株は両者ともボラティリティはゼロということになります。※

※ボラティリティの算定期間は0期から24期とします、同じ動きをしていても算出期間によってボラティリティの値は異なってきます。

投稿者: noguchi 日時: 16:56 | パーマリンク